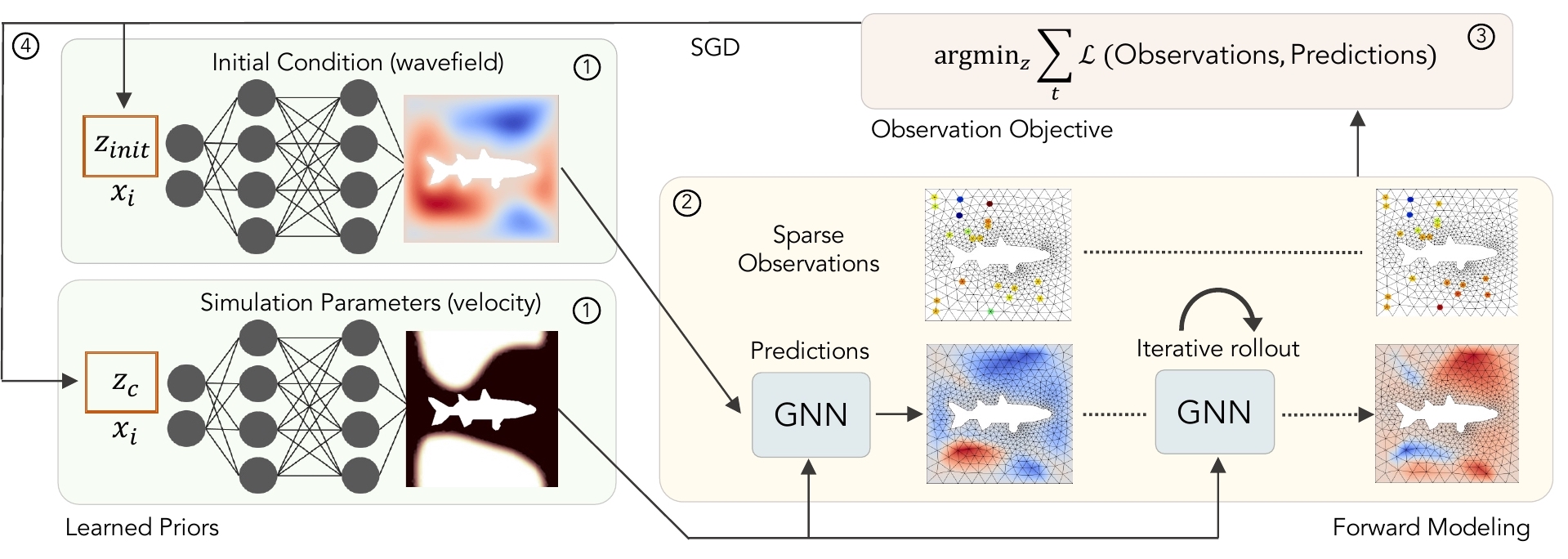
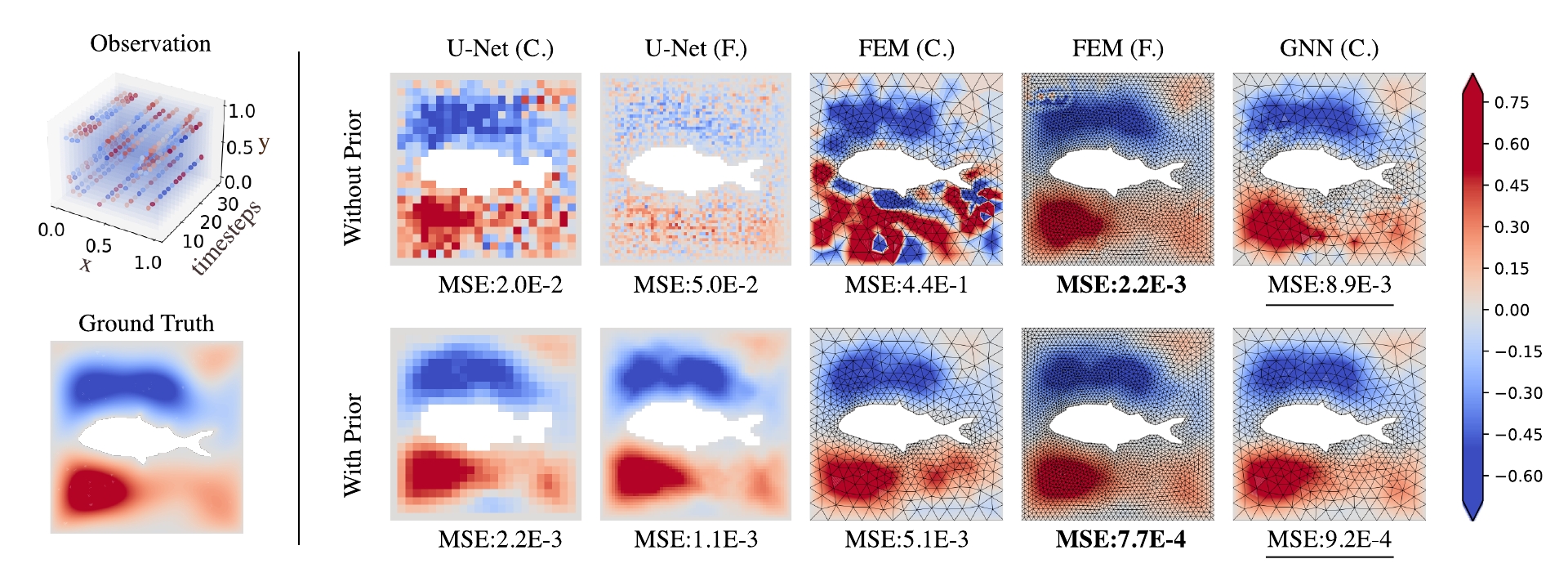
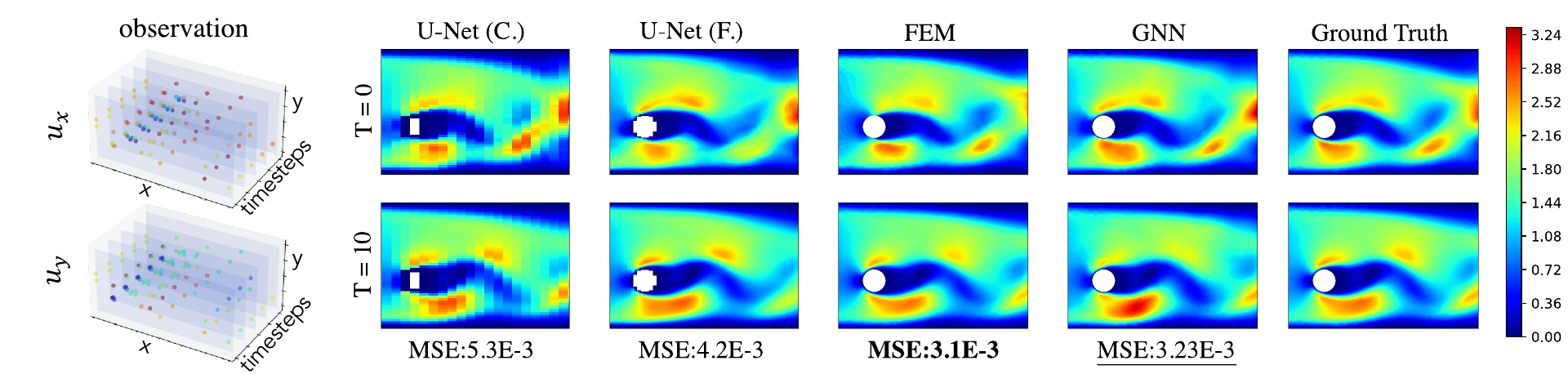
ABSTRACT
Learned graph neural networks (GNNs) have recently been established as fast and accurate alternatives for principled solvers in simulating the dynamics of physical systems. In many application domains across science and engineering, however, we are not only interested in a forward simulation but also in solving inverse problems with constraints defined by a partial differential equation (PDE). Here we explore GNNs to solve such PDE-constrained inverse problems. Given a sparse set of measurements, we are interested in recovering the initial condition or parameters of the PDE. We demonstrate that GNNs combined with autodecoder-style priors are well-suited for these tasks, achieving more accurate estimates of initial conditions or physical parameters than other learned approaches when applied to the wave equation or Navier-Stokes equations. We also demonstrate computational speedups of up to 90x using GNNs compared to principled solvers.